Наука без граница

ТАЈАНСТВЕНА ЗАВОДЉИВОСТ БРОЈЕВА

Заборављени систем бројева, измишљен још у 19. веку, могао би да пружи најједноставније објашњење зашто би наша васиона требало да има десет или једанаест димензија.

Сви смо учили о бројевима и о њиховом сабирању, одузимању, множењу и дељењу. Математичари знају да постоји више бројчаних система. Могу да се направе и вишедимензионални, али само у некима од њих изводљиве су све четири рачунске радње. Један такав случај чине „октониони” – осмодимензионални систем бројева стар преко 160 година. Ови необични бројеви данас добијају важност за суперсиметрију и теорију струна. И, ако су оне право објашњење за природу васионе, октониони би могли да потврде и објасне чудну бројност њених димензија. Ова занимљива замисао потекла је од математичара Џона Баеза и Џона Хуерте.

Надгорњавање математичара

   Размотримо најпре бројчани систем који математичари зову реалним бројевима. Скуп свих реалних бројева гради линију, налази се дуж једне праве, па зато можемо да кажемо да је једнодимензионалан. Ову замисао можемо и да преокренемо у тврдњу да је права једнодимензионална – зато што је довољан само један реалан број да би се на њој одредио положај.
   До 16. века реални бројеви били су „једини играч у граду”. Током ренесансе славољубиви математичари покушавали су да реше све сложеније једначине, такмичећи се ко је у томе најуспешнији. Квадратни корен од –1 био је тајно оружје италијанског математичара, физичара и астролога Ђиролама Кардана. Он је одважно користио овај тајанствени број тамо где су решења били обични реални бројеви. Није тачно знао зашто је његов трик успевао, већ само то да му је помагао да лакше дође до тачних решења.
    Своју замисао обелоданио је 1545. године, чиме је покренуо дуготрајна спорења. Да ли квадратни корен од –1 заиста постоји или је само варка? Готово сто година касније и велики мислилац и математичар Рене Декарт о томе је изрекао суд, дајући му донекле увредљиво име „имагинаран” број. Због тога ће се скраћено означавати малим словом і. Ипак, математичари су постепено кренули Кардановим стопама и почели да користе комплексне бројеве. То су бројеви у облику а + bi, где су а и b обични реални бројеви. Негде око 1806. године Жан Робер Арган први је изнео замисао да комплексни бројеви могу да опишу тачке у равни која је, за разлику од праве, дводимензионална.
   Како комплексни број а + bi описују тачку у равни? Једноставно – а нам говори колико је тачка удаљена, лево или десно, док нам b говори колико је померена горе или доле. Арган је отишао и корак даље разматрајући шта би уобичајене рачунске радње – сабирање, одузимање, множење и дељење – значиле за комплексне бројеве. Реални бројеви ће помоћи да лакше схватимо геометријски смисао комплексних бројева. Сабирање или одузимање било ког реалног броја у ствари је померање дуж линије реалних бројева – надесно или налево. Множење или дељење било којим позитивним бројем растеже, односно скупља ову праву. На пример, множењем са 2 она се растеже за чинилац 2, док је дељење са 2 сабија – померајући све тачке да постану двоструко ближе. Множење са –1 преврће праву.
   Слично важи и за комплексне бројеве – уз неке особености. Додавање било ког комплексног броја а + bi тачки у равни помера ту тачку надесно (или налево) за износ а, односно нагоре (или надоле) за износ b. Множење комплексним бројем развлачи или сабија раван. Међутим, новост је што је и заокреће (ротира)! Тако, множење са i ротира раван за четвртину круга. То значи да ако 1 помножимо са и два пута (i2), окрећемо раван за цео полукруг и добијамо –1. Дељење је супротна радња од множења – па имамо скупљање, а ротација тече у супротном смеру.
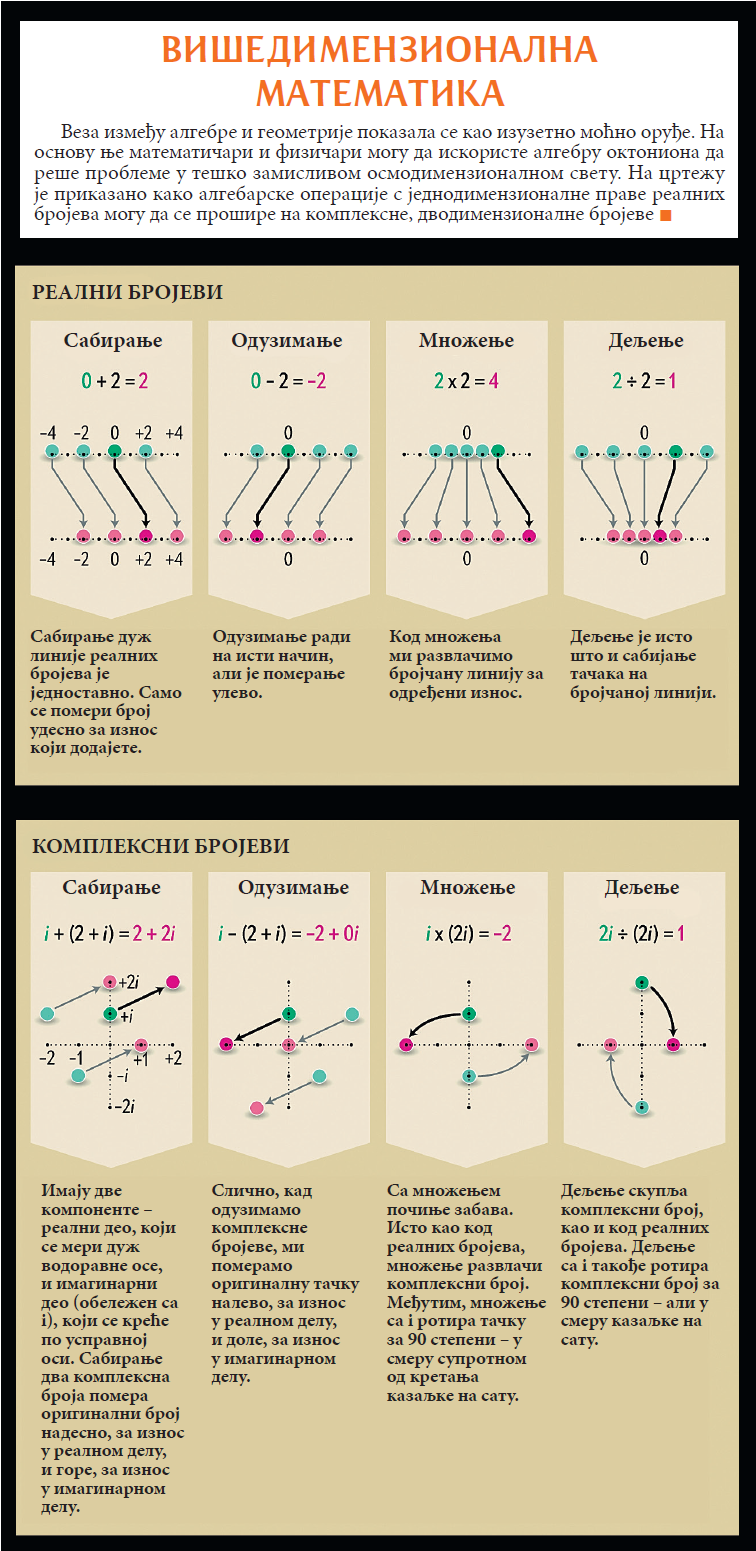   Готово све што можемо да урадимо с реалним бројевима можемо и с комплексним. У ствари, многе ствари теку боље, као што је то уочио и Кардано, јер можемо да решимо више једначина с комплексним бројевима него с реалним. Тако се наметнуло питање – ако је овај дводимензионални бројчани систем подарио већу моћ рачунања од једнодимензионалног, шта би могло да се очекује од бројчаних система са више димензија? Нажалост, показало се да је једноставно проширивање димензија бројчаних система немогуће. Тек ће, деценијама касније, један ирски математичар открити ову тајну. А данас, безмало два века касније, почињемо да схватамо колику би снагу ови системи могли да имају.

Формула у камену

   Године 1835, када је имао тридесет година, Вилијам Роуен Хамилтон (чувени ирски физичар, астроном и математичар, који је за научни допринос награђен племством), открио је да с комплексним бројевима може да се поступа као и с паровима реалних бројева. До тада су математичари већ уобичајили да комплексне бројеве пишу у облику а + bі, за шта се Арган и залагао. Хамилтон је приметио да не постоји препрека да се овај начин сведе на записивање два реална броја – на пример (а, b). То би омогућило да се комплексни бројеви врло лако сабирају или одузимају – довољно је да се то уради с одговарајућим реалним бројевима у пару.
   Затим је покушао да осмисли већу алгебру – алгебру триплета –тродимензионални бројчани систем у коме би могло да се сабира, одузима, множи и дели, а који би имао сличну улогу као комплексни бројеви, само у тродимензионалној геометрији. Међутим, тај вишегодишњи напор доносио му је само разочарања. Триплете је успевао да сабира и одузима, али не и да их множи и дели. У ствари, тада није знао да је такав задатак нерешив.
   Основни кривац било је дељење. Уосталом, зато системи бројева у којима је дељење могуће имају посебно име – „дивизиона алгебра”. Тек 1958. године тројици математичара успело је да докажу оно у шта се већ дуго сумњало – било која дивизиона алгебра мора да има једну димензију (реални бројеви), две (комплексни бројеви), четири или осам. Триплети нису на овом списку.
   Хамилтон је и сам открио своју заблуду. У октобру 1843. године, док је крај реке ишао ка Ирском краљевском друштву у Даблину, синула му је замисао. Толико значајна да је перорезом издубио њену формулу у камену моста Брум – да је не заборави. (Ту је касније постављена спомен-плоча – место ходочашћа многих математичара.) Хамилтон је схватио да – ротације, растезање и скупљање – у три димензије не могу да се опишу са само три броја. Потребан је и четврти, што значи и четвородимензионални бројчани низ – који је назвао кватерниони. Они би имали изглед а + bі + cj + dk, где би бројеви i, ј и k били три различита квадратна корена од –1.
   Можда изгледа чудно што су за опис промена у тродимензионалном простору потребни четвородимензионални бројеви. Али, три броја се потроше на описивање ротација, што најлакше може да се схвати на примеру авиона. Да бисмо управљали авионом прво морамо да утичемо на његов нагиб – угао према положеној равни (енг. pitch). Друго, требало би да дотерамо правац (енг. yaw), окрећући авион као и аутомобил – лево или десно. Треће, морамо да подесимо и угао авионских крила (енг. roll). Четврти број нам је потребан да опишемо растезање или скупљање.
   Опчињен кватернионима, Хамилтон је остатак живота утрошио на њихово проучавање, па је за њих нашао више корисних примена. Данас се кватерниони често замењују њиховим једноставнијим рођацима – векторима – који могу да се сматрају за кватернионе посебне класе: аи + бј + цк (само је први члан нула). Ипак, кватерниони остају незаобилазни чинилац када треба описати тродимензионалне ротације на рачунарима и појављују се свуда где је потребно – од управљања свемирским летелицама до графичких алата за видео игре.

Кршење закона артиметике

   Упркос тим применама, могли бисмо да се запитамо шта су тачно ј и k, ако смо већ  одредили да је i квадратни корен од –1. Да ли и ти квадратни корени од –1 заиста постоје?
   Можемо ли да измишљамо нове квадратне корене од –1 по жељи? Ова питања мучила су и Хамилтоновог школског друга, адвоката Џона Грејвса, који се аматерски бавио алгебром – и знатно утицао на Хамилтона да се окрене комплексним бројевима и триплетима. Зато није чудно што је још истог дана, када је у јесен 1843. године схватио у чему је грешио, Хамилтон пожурио да се похвали Грејвсу. Послао му је писмо у коме је детаљно описао своје откриће кватерниона. Грејвс му је одговорио недељу дана касније, честитао му, али и додао:
   „У систему и даље постоји нешто што ме збуњује. Још ми није јасно колики је опсег наше слободе да стварамо имагинарне бројеве и да их обдаримо натприродним својствима. Ако својом алхемијом можете да створите три фунте злата, зашто бисте на томе остали?”
   Ипак, Грејвс је оставио ове бриге по страни. Крајем децембра послао је друго  писмо Хамилтону у коме је објаснио свој осмодимензионални бројчани систем. Назвао га је октаве, а данас је познатији под именом октониони. Међутим, Хамилтон није показао веће занимање за њега. Није га пренео Ирском краљевском друштву како је обећао (што је тада био начин да се  објаве значајни математички резултати). Две године касније и даровити математичар Артур Кејли открио је октонионе и претекао Грејвса. Зато су октониони познати и као Кејлијеви бројеви.
   Зашто се Хамилтону нису свидели октониони? Прво, био је опседнут кватернионима. Али, имао је и чисто математички разлог – октониони су кршили неке уобичајене законе аритметике. Већ су кватерниони били помало чудни. Кад множите реалне бројеве, није важно који је редослед чинилаца – на пример, 2 помножено са 3 исто је што и 3 помножено са 2. Једнако важи и за комплексне бројеве. Математичари кажу да су, када је реч о множењу, ови бројеви „комутативни”. Међутим, то не важи за кватернионе – редослед је битан за крајњи резултат. То је зато што тада кватерниони описују ротације у три димензије, а редослед ротација утиче на крајњи исход.
    Лако можете и сами да се уверите у то. Узмите књигу окренуту предњом корицом према себи. Окрените је одозго надоле (тако да видите задњу корицу), а затим за четврт круга у правцу казаљке на сату (видећете бочну страну књиге, с листовима). Сада те радње (ротације) изведите обрнутим редоследом. Прво књигу окрените за четврт круга, а затим је преврните одозго надоле. Крајњи положај књиге биће другачији (видеће се њен повез).
   Октониони су још чуднији. Не само да су „некомутативни” као и кватерниони, већ крше још један уобичајени закон аритметике – „асоцијативност”. Она каже да је (хy)z = z (хy). Сви смо се уверили да је множење асоцијативно, али да постоје и неасоцијативне радње. На пример, (3–2)–1 је различито од 3–(2–1). Ипак, можда је најважнији разлог зашто је Хамилтон занемарио октонионе био тај што у то време није било јасно за шта би они могли да се употребе. У тесној су вези с геометријом од седам и осам димензија, па множећи октонионе могу да се опишу ротације у тим димензијама. Међутим, током више од једног века тај поступак био је само чисто интелектуално вежбање. Тек с развојем савремене физике честица – а посебно теорије струна – почело је да се назире колико би октониони могли да буду од користи и у стварном свету.

Уткани у ткиво природе

   Седамдесетих и осамдесетих година 20. века теоријски физичари су развили изузетно лепу замисао – суперсиметрију. (Касније ће и заговорници теорије струна схватити да и струне захтевају суперсиметрију.) Укратко, на најосновнијем стању васионе постоји симетрија између материје и сила. То значи да свака честица материје (на пример, електрон) има честицу близанца која преноси силу. Такође, свака честица преносилац силе (на пример, фотон – носилац електромагнетне силе) има близнакињу међу честицама материје.
   Према теорији суперсиметрије закони физике остаће непромењени ако заменимо честице материје с честицама преносиоцима сила, и обрнуто. Замислите да видите васиону у чудном огледалу које, уместо да мења лево за десно, размењује сваку честицу силе с честицом материје и обрнуто. Ако је суперсиметрија тачна, ако заиста описује нашу васиону, ова васиона-огледало понашала би се исто као и наша.
    Према квантној механици честице су и таласи. У уобичајеној тродимензионалној верзији квантне механике, коју физичари свакодневно користе, једна врста бројева (спинори) описује таласно кретање материјалних честица. Друга врста (вектори) описује таласно кретање честица преносилаца сила. Да би се разумела међудејства честица неопходно је да се ове две врсте бројева спајају, множе. Иако је начин како се то данас ради можда успешан – нимало није једноставан.
    Као другу могућност замислите чудну васиону у којој не постоји време, већ само простор. Ако та васиона има димензије – једну, две, четири или осам – обе врсте честица (и материје и сила) биле би таласи које описује само једна врста бројева. Односно, бројеви из неке од дивизионих алгебри – једине врсте бројчаних система који омогућавају све четири радње (сабирање, одузимање, множење и дељење). Другим речима, у овим бројчаним димензијама спинори и вектори се подударају – само су (истим редоследом) реални бројеви, комплексни бројеви, кватерниони или октониони. Тада суперсиметрија природно извире обезбеђујући обједињено објашњење материје и сила у васиони. Једноставно множење описује њихова међудејства и за све честице, без обзира на врсту, користи се исти систем бројева. Ипак, оваква васиона не постоји, јер у обзир мора да се узме и време.
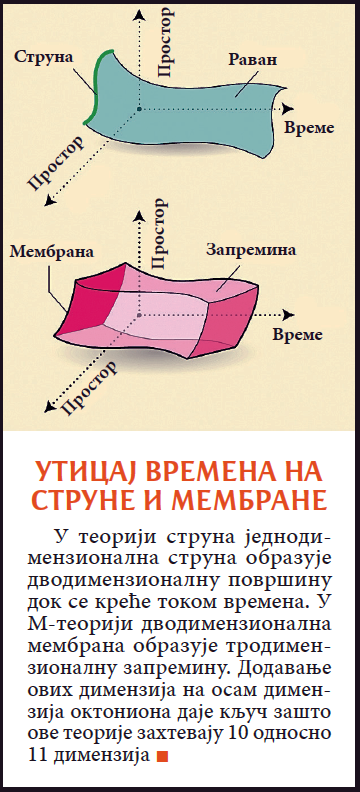
   Када је у питању теорија струна, разматрање времена има занимљиву последицу. У било ком тренутку струна је једнодимензионални објекат – као што су крива линија или права. Међутим, како време протиче, струне у кретању образују траг у виду дводимензионалних површина. Ова чињеница мења број димензија у којима се суперсиметрија јавља – додајући две – једну за струне и једну за време. И тако, уместо суперсиметрије у једној, две, четири или осам димензија – добијамо суперсиметрију у три, четири, шест и 10 димензија.
   Занимљиво је да теоретичари струна већ годинама сматрају да је само  десетодимензионална верзија теорије самоодржива. Остале имају озбиљну ману – да израчунавање истих ствари на два различита начина даје различите резултате. У било којој другој, осим у десет димензија, теорија струна се руши. А теорија струна с десет димензија користи октонионе. Васиона мора да има 10 димензија – јер су у десет димензија све честице материје и сила обухваћене истом врстом бројева – октонионима!
   Међутим, ово није крај приче. Физичари су кренули даље и од струна – почевши да разматрају „мембране”. У одређеном тренутку, дводимензионална мембрана личи на лист хартије. С протоком времена она образује тродимензионалну запремину у простор-времену. Зато, за разлику од теорије струна (где треба додати две димензије), овде треба додати три. А суперсиметрија би требало да се јавља у димензијама: четири, пет, седам и 11. И, ето опет изненађења!
    Као и у случају струна, и овде се то уклапа у предвиђања теоретичара – да М-теорија („М” је мембрана) захтева 11 димензија. А то значи да би и ова теорија требало да користи октонионе. Нажалост, још је нико добро не разуме, нити зна које су њене основне једначине. Зато се ово „М” често чита и као „мистериозна”. Ипак, ни теорија струна, ни М-теорија до сада немају ниједан огледни доказ. Још су само леп сан теоретичара. Насупрот томе, васиона коју видимо не изгледа као да има 10 или 11 димензија, нити је откривена симетрија између честица материје и честица сила. Теоретичари струна полажу наду у Велики хадронски сударач честица крај Женеве. Дејвид Грос, један од водећих, процењује да је вероватноћа за откриће суперсиметрије око 50 одсто.
   Други стручњаци сматрају да је много мања. Време ће бити судија и у питању да ли су октониони од пресудне важности за разумевање света или су само делић заводљиве математике. Наравно, и математичка лепота има вредност, али би било још много боље ако би се испоставило да су октониони уткани у само ткиво природе. И, као што примери с комплексним бројевима и другим математичким достигнућима показују, не би било први пут да је неко чисто математичко откриће постало корисна алатка у рукама физичара и космолога .